1. 傅里叶变换原理

傅里叶变换的核心是从时域到频域的变换，而这种变换是通过一组特殊的正交基来实现的。

1.1 时域

时域是描述一个数学函数或物理信号对时间的关系，这也是日常中最容易直观感受的一种域。从我们学物理开始，很多物理量的定义都是跟时间相关的。

• 速度：位移与发生位移所用时间只比
• 电流：单位之间里通过导体任一横截面的电量
• 功率：物体在单位时间里做的功
• 等等

很多物理量的定义都是基于单位时间产生的效果或者变化，以时间为参考让我们更容易理解。但是容易理解不代表方便使用，或者说方便计算。

比如一段音频的波形图：

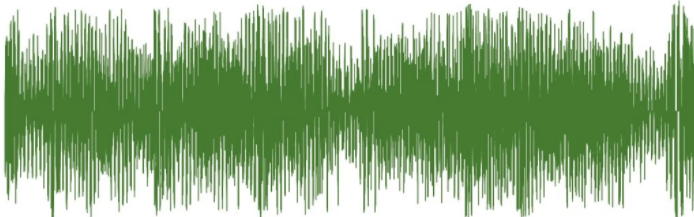
横轴为时间t，纵轴为振幅A[-1, 1]。假设播放器读入这段音频进行音频播放。现在我想让音量大一些，播放器应该怎么做呢？

因为上面的波形图的振幅对应的其实就是声音的强度，如果想让音量大一些，只需要将整体的振幅同比例扩大即可。这个需求看起来很容易满足。

但如果我比较喜欢低音效果，虽然音色已经比较低了，但是我还是想加强上面这段音乐的低音部分，更加厚重一些，那播放器应该怎么做呢？

虽然这是一段美妙的音乐，但是从时域的图像看起来，似乎杂乱无章，想找到低音部分根本无从下手，跟不用说将低音部分加强了。因为高中低音在时域中是杂糅在一起的，我们无法将他们剥离开来，随便改动波形图中的一小部分，都会同时影响到高中低音。所以如果播放器仅仅对时域信号进行处理是无法完成这个需求的。

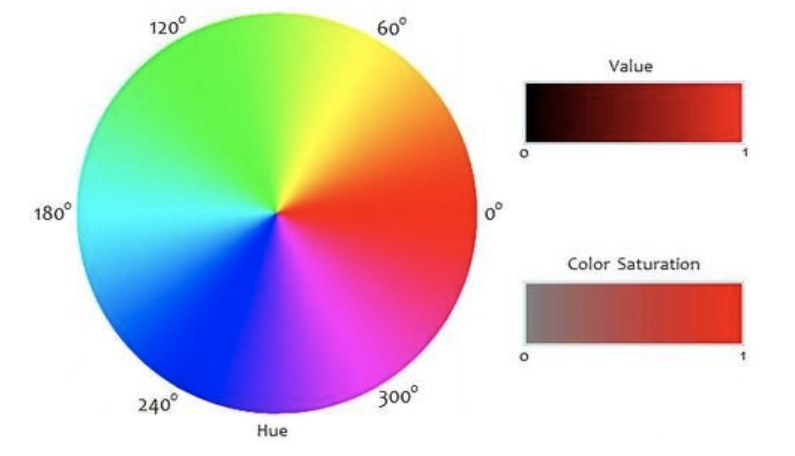
和时域的这种限制类似的还有RGB空间。任何一个颜色都可以通过R/G/B(红/绿/蓝)三原色表示出来。如下图。

通过调整三种颜色的配比，就能混合出各种颜色。为什么我们经常通过RGB空间来表示所有的颜色呢？因为人类有三种视锥细胞，而这三种视锥细胞最敏感的波长接近于红/绿/蓝（如下图）。所以任何颜色对于大脑来说，都是这三种视锥细胞电信号的混合作用。这也是我们使用RGB空间的生物学基础。

虽然RGB空间和我们的视锥细胞原理类似，而且模型非常简单。但是在某些条件下，它仍然无法满足我们的需求。比如，我们在拍照时有时会出现红眼现象。我们需要PS掉红眼，但是我们如何在RGB空间中找到红色的范围呢？有人可能会说，R值越大的地方代表越红，是这样的吗？我们看(R,G,B)=(170, 0, 0)时，颜色如下：

上图的颜色我们可以认为是红色的范围。但当RGB=(187, 187, 187)的时候，颜色如下图所示：

虽然R的值增大了，但是G/B值的大小也会影响混合的颜色，导致变成了灰色。所以RGB三个值，牵一发而动全身，如果想在RGB空间找到红色范围是非常困难的，这就需要将色彩从RGB空间转换到HSV空间（如下图，这里不做详述），在HSV空间红色的范围可以很容易的表示出来。

RGB空间就和时域一样，都有着自身的限制。所以最容易理解的表现形式并不一定是最方便计算的。我们往往需要进行一种变换，将在原来空间中难以处理的问题变换到方便计算的空间中去。

1.2 频域

频域就是描述频率所用到的空间或者说坐标系。频率虽然比较抽象，但是在我们的生活中是无处不在的，只是我们很少直接提到这个专业名词。

对于波来说，频率是每秒波形重复的数量。声音是一种波；光具有波粒二象性，也具有电磁波的性质；更普遍的说，频率是物质每秒钟完成周期性变化的次数。比如家里用的交流电是50Hz，意思就是电压每秒完成50次振荡周期，如下图：

而前面提到的低音效果是什么样的效果呢？就好比家庭影院中的低音炮，它是如何实现重低音的呢？简单来说，可以将它简化成一个低通滤波器，下图是低通滤波器的频率响应曲线：

横轴是频率(Hz)，纵轴是声音大小(dB)。（请忽略图中的频率刻度，没有对应人声的频率范围）

所谓的低音效果，其实就是对人声中的低音部分保留或增强，对应上图中左侧的横线部分；而对于人声中的高音部分进行衰减，对应上图中右侧的斜坡部分。通过这个低通滤波器，我们就能将低音过滤，将高音衰减。为了实现更好的视听效果，实际中，功放或播放器的实现会比这个复杂得多，上图中进行了极简化。

可见，低音效果是在频率范围内考虑问题，而波形图是在时域内的图像，所以如果想在时域内解决低音效果的问题，就如同鸡同鸭讲。所以我们要就要找到一个沟通时域和频域的桥梁，也就是一个翻译，让时域和频域能够无障碍的沟通。但是，时域和频域表达的又只能是同一种信息，只是表现形式不同。

1.3 时域转频域

先来看一下标准正弦函数，如下图：

在时域它的函数方程是 ：

y = sin(x)

 而它的频率是 ：

f = \frac{1}{T} = \frac{1}{2π}

 所以，上面这个函数在频域中的图像如下：

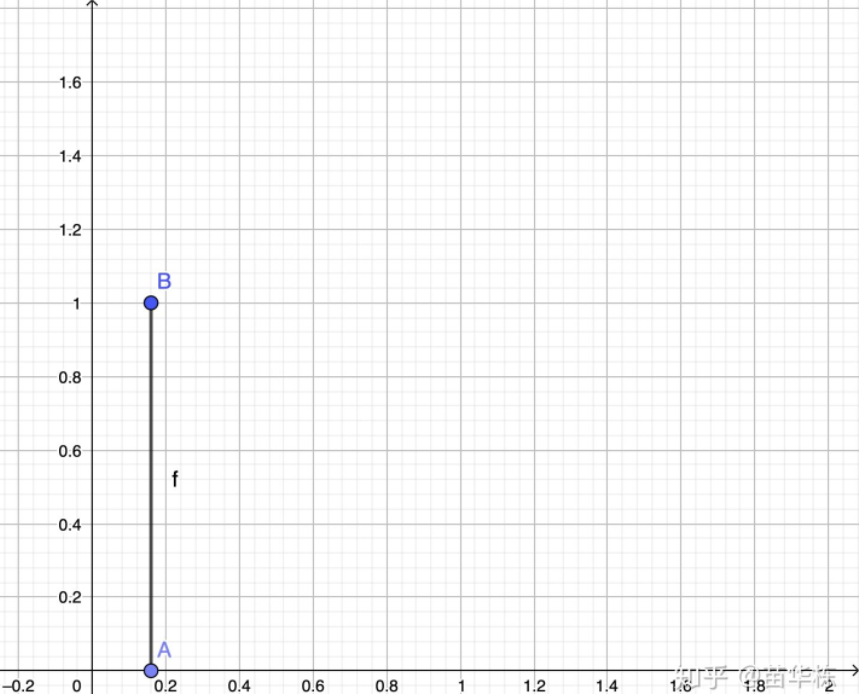
横轴是频率f，纵轴是幅值A。上面两张图分别从时域和频域展示了正弦函数，但表达的都是同样的信息。

再来一个更明显的例子：

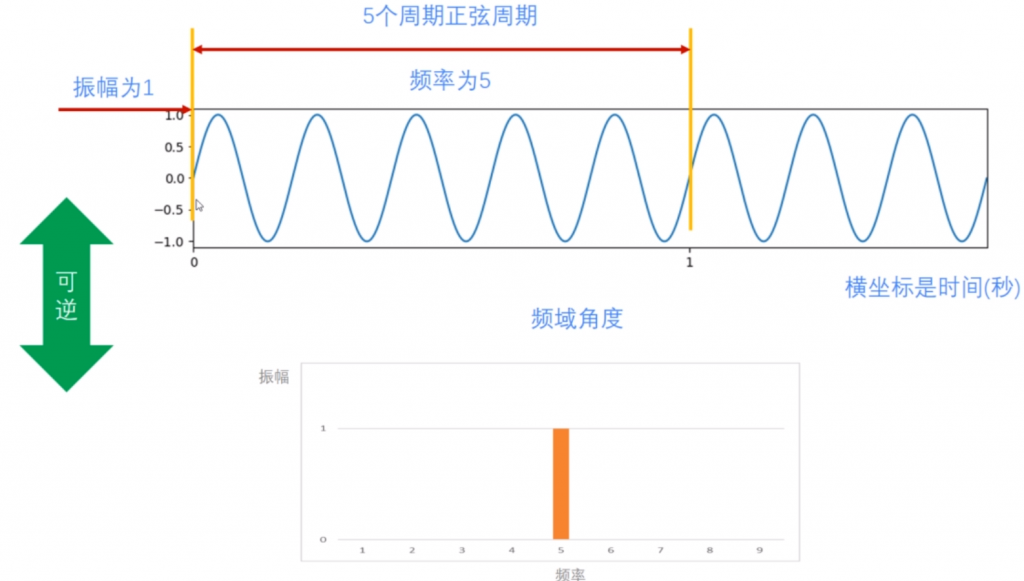
由于正弦函数是单一频率，在频域中只需要一根竖线就能表现出来。我们期望的也是将时域的信号转换成一个个单一频率的正弦函数的组合，这样我们就能够在频域中用一根根竖线表示出来，也就完成了从时域到频域的转换。

例如将：

y = Asin(2πfx + Φ)

转化为：

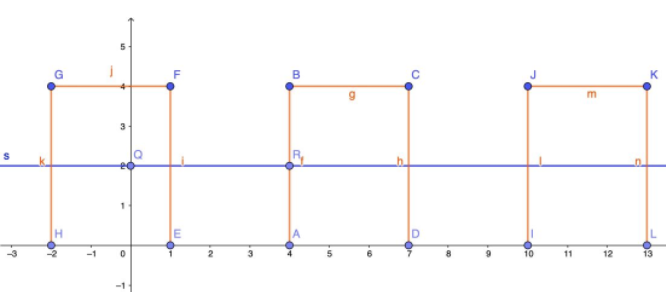
y = Asin(2πfx + θ) = Asin(θ)cos(2πfx) + Acos(θ)sin(2πfx) = a_{n}cos(2πfx) + b_{n}sin(2πfx)

别急… 实际的波形可能会有一个”直流分量“，如下图。这个方形波并没有沿X轴往复运动，而是沿Y = 2 这条直线往复运动。对于这类的波形，单纯的用正余弦函数组合是无法表示出来的，因为正余弦都是沿X轴往复运动，所以必须叠加一个”直流分量“。

所以最后，如果任意波形都可以转化成常数、若干个正余弦函数的线性组合，我们就可以完成时域到频域的转换。用数学公式表达如下面所示：

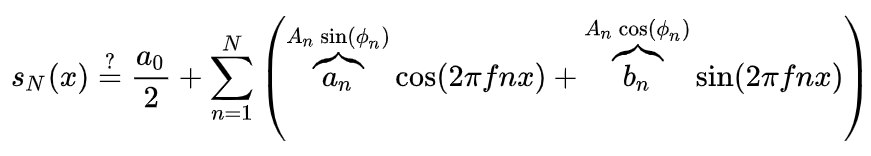
上式中的直流分量我们可以把它想象成一个常数而已。于是问题就转化成，对于任意波形，我们能不能找到一组系数an和bn使上述等式成立。

到这里，法国数学家傅里叶就必须登场了。他在1807年发表的论文中帮我们完成了这个工作，他提出了一个当时非常具有争议性的论断：任何连续周期信号都可以由一组适当的正弦曲线组合而成。

其实，对于连续周期信号，比如上图中的周期方波，严格意义上说它的频域变换叫做傅里叶级数，因为经过频域变换后，它的频谱是离散的。而当我们现在说起傅里叶变换，默认指的是连续非周期信号的变换。因为非周期信号可以想象成信号的周期趋近于无穷大，所以傅里叶变换其实是对傅里叶级数的扩展。

2. 傅里叶变换的实现

2.1 Numpy实现傅里叶变换

numpy.fft.fft2

• 实现傅里叶变换
• 返回一个复数数组(complex ndarray)

numpy.fft.fftshift

• 将零频率分量移到频谱中心

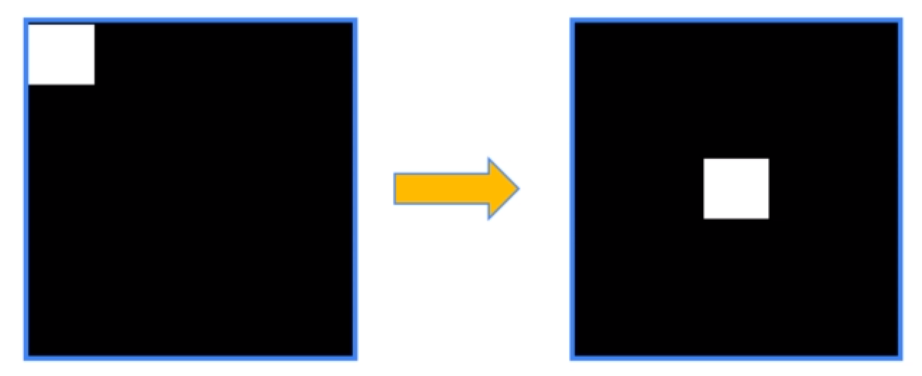
20*np.log(np.abs(fshift))

• 设置频谱的范围

import cv2
import matplotlib.pyplot as plt
import numpy as np

img1 = cv2.imread('lenna.jpg', cv2.IMREAD_GRAYSCALE)
#第一步
f = np.fft.fft2(img1)
#第二步
fshift = np.fft.fftshift(f)
#第三步
result = 20*np.log(np.abs(fshift))

#对比原始图像与傅里叶图像
plt.subplot(121)
plt.imshow(img1, cmap = 'gray')
plt.title('original')
plt.axis('off')

plt.subplot(122)
plt.imshow(result, cmap = 'gray')
plt.title('result')
plt.axis('off')
plt.show

• 注意：
  • 傅里叶得到低频高频信息，针对低频高频处理能够实现不同的目的。
  • 傅里叶过程是可逆的，图像经过傅里叶变换，逆傅里叶变换后，能够恢复到原始的图像。
  • 在频域对图像进行处理，在频域的处理会反应在逆变换图像上。

2.2 Numpy实现逆傅里叶变换

numpy.fft.ifft2

• 实现傅里叶逆变换
• 返回一个复数数组(complex ndarray)

numpy.fft.ifftshift

• 将零频率分量移到左上角

iimg = np.abs(逆傅里叶变换结果)

• 设置值的范围[0, 255]

import cv2
import matplotlib.pyplot as plt
import numpy as np

img1 = cv2.imread('lenna.jpg', cv2.IMREAD_GRAYSCALE)
#先变过去
f = np.fft.fft2(img1)
#零频率分量居中
fshift = np.fft.fftshift(f)

#第一步，将居中的零频率分量还原到左上
ishift = np.fft.ifftshift(fshift)
#第二步，逆傅里叶变换（返回负数数组）
iimg = np.fft.ifft2(ishift)
#第三步，取绝对值转换为实数
iimg = np.abs(iimg)
#result = 20*np.log(np.abs(fshift))

plt.subplot(121)
plt.imshow(img1, cmap = 'gray')
plt.title('original')
plt.axis('off')

plt.subplot(122)
plt.imshow(iimg, cmap = 'gray')
plt.title('result')
plt.axis('off')
plt.show

2.3 高通滤波演示

• 低频对应图像内变化缓慢的灰度分量。例如，在一副大草原的图像中，低频对应着颜色趋于一致的草原。衰减低频通过高频，高通滤波器，将增强尖锐的细节，但是会导致图像对比度的降低。
• 高频对应图像内变化越来越快的灰度分量，是有灰度的尖锐过度造成的。在草原图像中代表的是羊群的边缘等信息。衰减高频通过低频，低通滤波器，将模糊一副图像。

频域滤波：修改傅里叶变换已达到特殊目的，然后计算逆傅里叶变换返回到图像域。特殊目的：图像增强，去噪，边缘检测，特征提取，压缩，加密等。

import cv2
import matplotlib.pyplot as plt
import numpy as np

img1 = cv2.imread('lenna.jpg', cv2.IMREAD_GRAYSCALE)
#先变过去
f = np.fft.fft2(img1)
#零频率分量居中
fshift = np.fft.fftshift(f)
#根据中心，将选定部分过滤（设置成0）
rows, cols = img1.shape
crow, ccol = int(rows/2), int(cols/2)
fshift[crow - 30: crow + 30, ccol - 30: ccol + 30] = 0

#还原
ishift = ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)

plt.subplot(121)
plt.imshow(img1, cmap = 'gray')
plt.title('original')
plt.axis('off')

plt.subplot(122)
plt.imshow(iimg, cmap = 'gray')
plt.title('result')
plt.axis('off')
plt.show

2.4 OpenCV实现傅里叶变换

返回结果 = cv2.dft(原始图像，转换标识)

• 返回结果：是双通道的。第一个通道结果是实数部分；第二个通道结果是虚数部分。
• 原始图像：输入图像首先要转换成np.float32格式。使用np.float32(img1)
• 转换标识：flags = cv2.DFT_COMPLEX_OUTPUT,输出一个复数阵列。

numpy.fft.fftshift

• 将零频率分量移到频谱中心

返回值 = cv2.magnitude(参数1， 参数2)

• 双通道转换为8位的位图。
  • 参数1，浮点型X坐标值，也就是实部。
  • 参数2，浮点型Y坐标值，也就是虚部。

import cv2
import matplotlib.pyplot as plt
import numpy as np

img1 = cv2.imread('lenna.jpg', cv2.IMREAD_GRAYSCALE)

#第一步，傅里叶变换
dft = cv2.dft(np.float32(img1), flags = cv2.DFT_COMPLEX_OUTPUT)
#第二步，低频移到中间
dftShift = np.fft.fftshift(dft)
#第三步，双通道转灰度，然后取log乘以20变到0-255范围。
result = 20*np.log(cv2.magnitude(dftShift[:, :, 0], dftShift[:, :, 1]))

plt.subplot(121)
plt.imshow(img1, cmap = 'gray')
plt.title('original')
plt.axis('off')

plt.subplot(122)
plt.imshow(result, cmap = 'gray')
plt.title('result')
plt.axis('off')
plt.show

2.5 OpenCV实现逆傅里叶变换

返回结果 = cv2.idft(原始数据)

• 返回结果：取决于原始数据的类型和大小。
• 原始数据：实数或者负数均可。

返回值 = cv2.magnitude(参数1， 参数2)

• 双通道转换为8位的位图。
  • 参数1，浮点型X坐标值，也就是实部。
  • 参数2，浮点型Y坐标值，也就是虚部。

numpy.fft.ifftshift

• 将零频率分量移到左上角

import cv2
import matplotlib.pyplot as plt
import numpy as np

img1 = cv2.imread('lenna.jpg', cv2.IMREAD_GRAYSCALE)
#先变过去
dft = cv2.dft(np.float32(img1), flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)


#第一步，低频位置还原
ishift = np.fft.ifftshift(dftShift)
#第二步，逆傅里叶变换
iimg = cv2.idft(ishift)
#第三步，合并通道转化颜色区间
iimg = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1])

plt.subplot(121)
plt.imshow(img1, cmap = 'gray')
plt.title('original')
plt.axis('off')

plt.subplot(122)
plt.imshow(iimg, cmap = 'gray')
plt.title('result')
plt.axis('off')
plt.show

2.6 低通滤波演示

原理和掩膜相同。

import cv2
import matplotlib.pyplot as plt
import numpy as np

img1 = cv2.imread('lenna.jpg', cv2.IMREAD_GRAYSCALE)

#傅里叶变换
dft = cv2.dft(np.float32(img1), flags = cv2.DFT_COMPLEX_OUTPUT)
dftShift = np.fft.fftshift(dft)


#制作掩膜，中间挖空（值不为0）
rows, cols = img1.shape
crow, ccol = int(rows/2), int(cols/2)
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow - 30: crow + 30, ccol - 30: ccol + 30] = 1

#应用掩膜
fshift = dftShift * mask


#逆傅里叶变换
ishift = np.fft.ifftshift(fshift)
img2 = cv2.idft(ishift)
img2 = cv2.magnitude(img2[:, :, 0], img2[:, :, 1])

plt.subplot(121)
plt.imshow(img1, cmap = 'gray')
plt.title('original')
plt.axis('off')

plt.subplot(122)
plt.imshow(img2, cmap = 'gray')
plt.title('result')
plt.axis('off')
plt.show

• OpenCV
• 计算机视觉