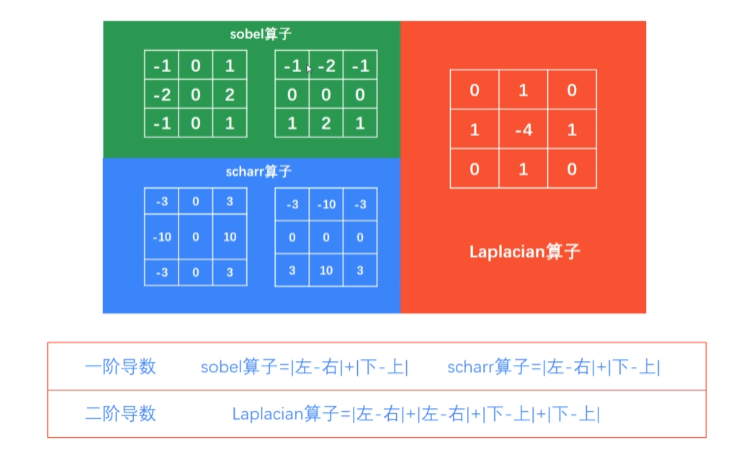
1.sobel算子的理论基础

索贝尔算子（Sobel operator）主要用作边缘检测，在技术上，它是一离散性差分算子，用来运算图像亮度函数的灰度之近似值。

Sobel卷积因子

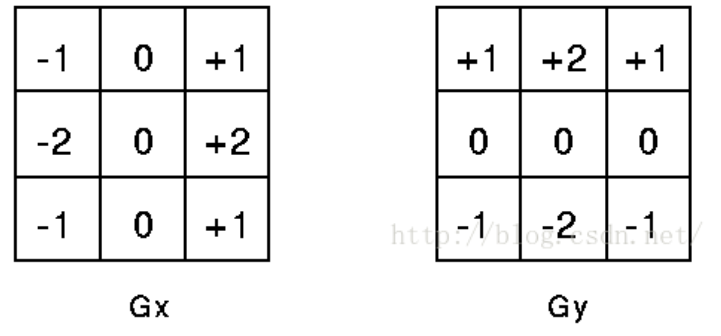
该算子包含两组3×3的矩阵，分别为横向及纵向，将之与图像作平面卷积，即可分别得出横向及纵向的亮度差分近似值。如果以A代表原始图像，Gx及Gy分别代表经横向及纵向边缘检测的图像灰度值。

从右往左，从上往下：

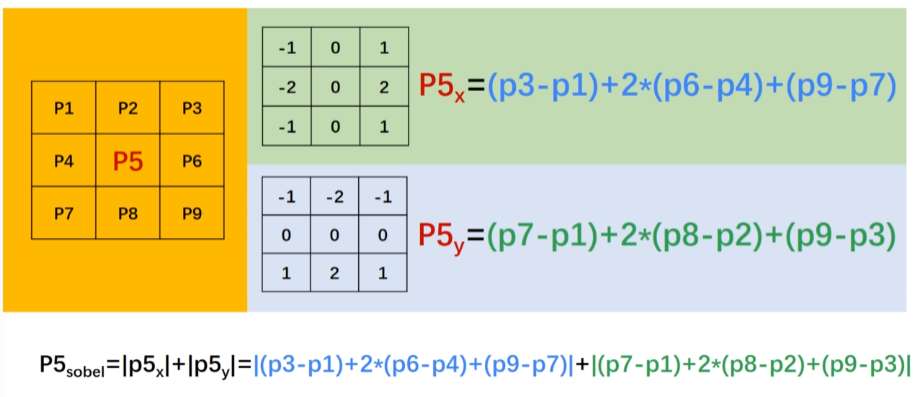
G =\sqrt{(G_x)^2 + (G_y)^2}

简化版本：

G =|G_x| + |G_y|

2.Sobel算子的函数及应用

#img2 = cv2.Sobel(img1, ddepth, dx, dy, [ksize])
#ddepth:处理结果图像深度，通常为-1，让处理结果与原图像始终保持一致
#dx:x轴方向,计算x方向梯度：[dx = 1, dy = 0]
#dy:y轴方向，计算y方向梯度：[dx = 0, dy = 1]
#ksize:核大小,设置为奇数。默认为3

#计算sobel方式1：dx = 1, dy = 1 (不严谨不推荐)
img2 = cv2.Sobel(img1, -1, 1, 1)

#计算sobel方式2：分别计算dx和dy后相加
dx = cv2.Sobel(img1, ddepth, 1, 0)
dy = cv2.Sobel(img1, ddepth, 0, 1)
#img2 = dx*系数1 + dy*系数2 #乘以系数主要是防止溢出，一般系数为0.5
#img2 = cv2.addWeighted(dx, alpha, dy, beta, gamma)
img2 = cv2.addWeighted(dx, 0.5, dy, 0.5, 0)

上述代码有一个问题，即只会抓取右边界和下边界。左上边界因为负数原因没有被成功抓取。所以，在计算时，使用更高的数据类型cv2.CV_64F，取绝对值后再转换成np.unit8（cv2.CV_8U）。所以深度ddepth不写-1，改cv2.CV_64F。整体流程如下：

#第一步，使用更高数据类型
sobelx = cv2.Sobel(img1, cv2.CV_64F, 1, 0)
sobely = cv2.Sobel(img1, cv2.CV_64F, 0, 1)

#第二步，取绝对值，并将梯度图像转换成256色位图，转换为unit8类型
#img2 = cv2.convertScaleAbs(img1, [, alpha[, beta]])
#目标图像 = 调整（原始图像 * aplha + beta）
#或者
#img2 = cv2.convertScaleAbs(img1)
sobelx= cv2.convertScaleAbs(sobelx)
sobely= cv2.convertScaleAbs(sobely)

#第三步，相加x和y的梯度
img2 = cv2.addWeighted(sobelx, 0.5, sobely, 0.5, 0)

3.Scharr算子的函数及其应用

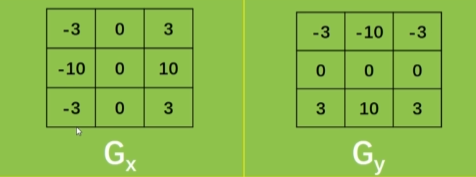
类似sobel算子，但是系数不一样。

#img2 = Scharr(img1, ddpeth, dx, dy)

#第一步，使用更高数据类型
scharrx = cv2.Scharr(img1, cv2.CV_64F, 1, 0)
scharry = cv2.Scharr(img1, cv2.CV_64F, 0, 1)

#第二步，取绝对值，并将梯度图像转换成256色位图，转换为unit8类型
#img2 = cv2.convertScaleAbs(img1, [, alpha[, beta]])
#目标图像 = 调整（原始图像 * aplha + beta）
#或者
#img2 = cv2.convertScaleAbs(img1)
scharrx = cv2.convertScaleAbs(scharrx)
scharry = cv2.convertScaleAbs(scharry)

#第三步，相加x和y的梯度
img2 = cv2.addWeighted(scharrx, 0.5, scharry, 0.5, 0)

Sobel对大的色差比较敏感，Scharr对于小的差值也能很好的反映出来。

4.Laplacian函数及其使用

图像处理经常把Laplace算子作为边缘检测之一，也是工程数学中常用的一种积分变换。拉普拉斯算子（Laplace Operator）是n维欧几里得空间中的一个二阶微分算子，定义为梯度(∇f)的散度(∇⋅)。

\Delta f = \nabla^2f = \nabla \cdot \nabla f= div(gradf)

在笛卡尔坐标系下，拉普拉斯算子可以被表示为：

\Delta f = \frac{\partial^2f}{\partial x^2} + \frac{\partial^2f}{\partial y^2} + \frac{\partial^2f}{\partial z^2}

推广到n维空间中的形式为:

\Delta = \sum \limits_{i} \frac{\partial^2f}{\partial x^2_i}

现在用散度的概念解读一下：

• 如果 Δf=0Δf=0 ，可以近似认为中心点 f(x,y)f(x,y) 的势和其周围点的势是相等的， f(x,y)f(x,y)局部范围内不存在势差。所以该点无源。
• Δf>0Δf>0 ，可以近似认为中心点 f(x,y)f(x,y) 的势低于周围点，可以想象成中心点如恒星一样发出能量，补给周围的点，所以该点是正源
• Δf<0Δf<0 ,可以近似认为中心点 f(x,y)f(x,y) 的势高于周围点，可以想象成中心点如吸引子一样在吸收能量，所以该点是负源

OpenCV中的Laplacian函数：

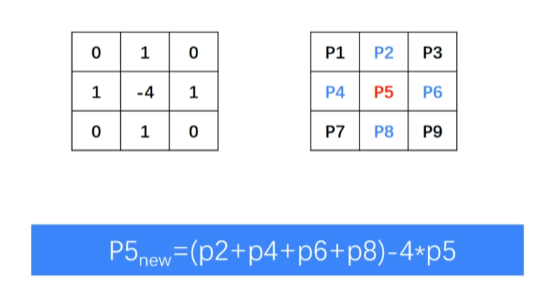
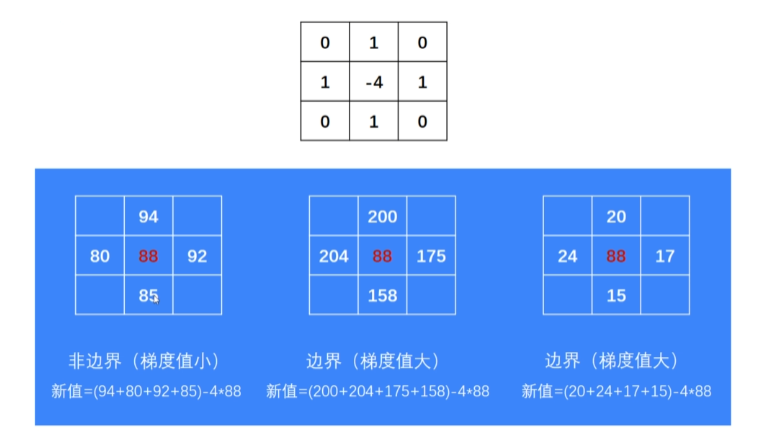
对比sobel算子和scharr算子：

#img2 = cv2.Laplacian(img1, ddepth)

#第一步，使用更高数据类型
laplacian= cv2.Laplacian(img1, cv2.CV_64F)

#第二步，取绝对值，并将梯度图像转换成256色位图，转换为unit8类型
img2= cv2.convertScaleAbs(laplacian)

5.Canny边缘检测原理

Canny边缘检测一般分为四步：

1. 去噪：边缘检测容易受到噪声的影响，因此在检测前通常需要进行去噪。一般使用高斯滤波器去除噪声。
2. 梯度：梯度方向一般总是与边界垂直。被归为四类：垂直，水平与两个对角线。用Angle(θ) = tan-1(Gy/Gx)获得。
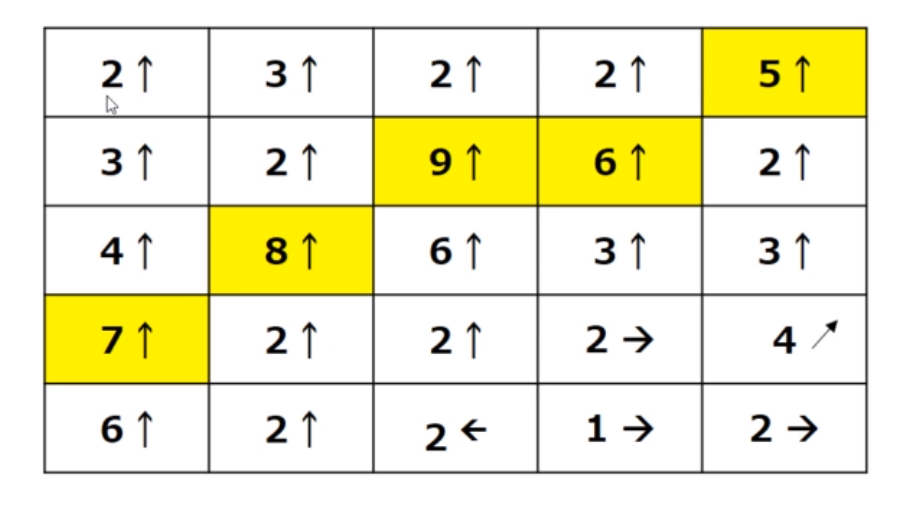
3. 非极大值抑制：遍历像素点，判断当前像素点是否是周围像素点中具有相同方向梯度的最大值。
4. 滞后阈值。详见后文。

非极大值抑制：点A,B,C具有相同方向，梯度方向垂直于边缘。判断点A是否为点A,B,C的局部最大值。如果是，则保留该点，否则它被抑制（清零）。

滞后阈值：小于给定最小阈值的边界值抛弃，大于最大阈值的边界值判定为边界。在最大最小阈值之间的，若与大于最大阈值的边界相连则判定为边界；反之则抛弃。

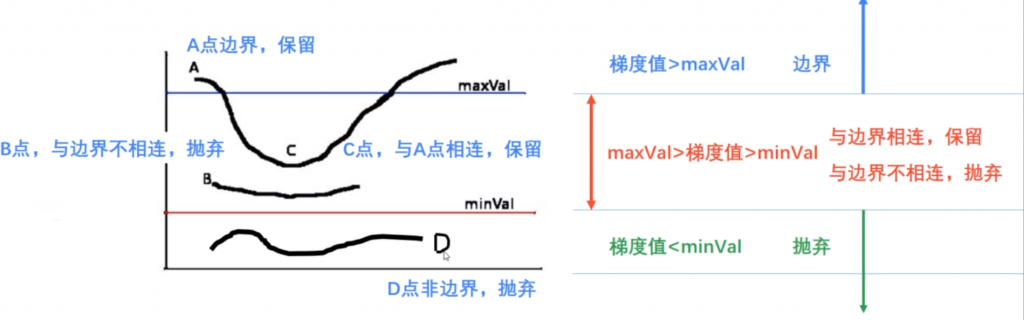
6.Canny函数及其使用

#img2 = cv2.Canny(img1, 阈值1, 阈值2)
#阈值1：minVal, 阈值2：maxVal
#阈值越小，边界信息越丰富，细节越多。

img2 = cv2.Canny(img1, 100, 200)

• OpenCV
• 计算机视觉