​图像滤波，即在尽量保留图像细节特征的条件下对噪声进行抑制，通过抑制高频段来减少噪音，同时会照成图像一定程度上的模糊，这也叫做平滑或者低通滤波器。

滤波本来应该是在傅立叶变换的频谱上对图像进行处理。但由于傅立叶的卷积特性

F[g*h]=F[g]F[h]

滤波后的图像可以由原图像和滤波算子做卷积生成（频域的乘积 => 空域的卷积）

g*h=F^{-1}[F[g]F[h]]

更多有关傅里叶变换，参考如下视频：

1.均值滤波

任意一点的像素值，都是周围N*N个像素值的均值。

下图是一个5*5的均值滤波核：

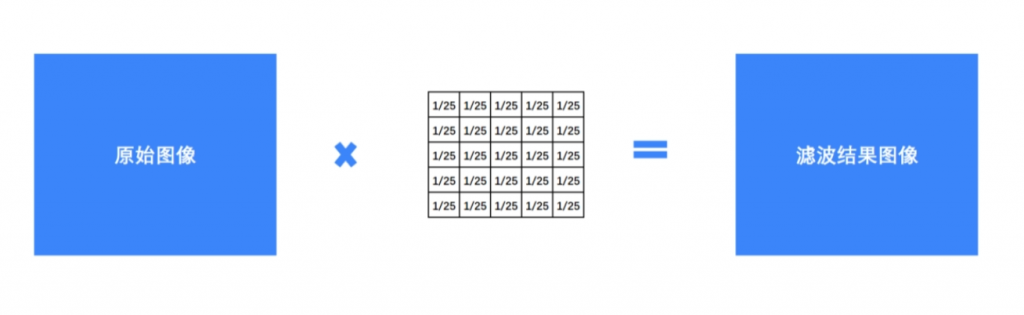
#处理结果 = cv2.blur(原始图像，核大小)
#核大小：以（宽度，高度）形式表示的元组
#因为会模糊，所以可以去除噪点

img2 = cv2.blur(img1, (5, 5))

缺陷：均值滤波本身存在着固有的缺陷，即它不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变得模糊，不能很好地去除噪声点。特别是椒盐噪声

2.方框滤波

与均值滤波的主要区别是多了一个归一化处理。若归一化则与均值滤波一样。

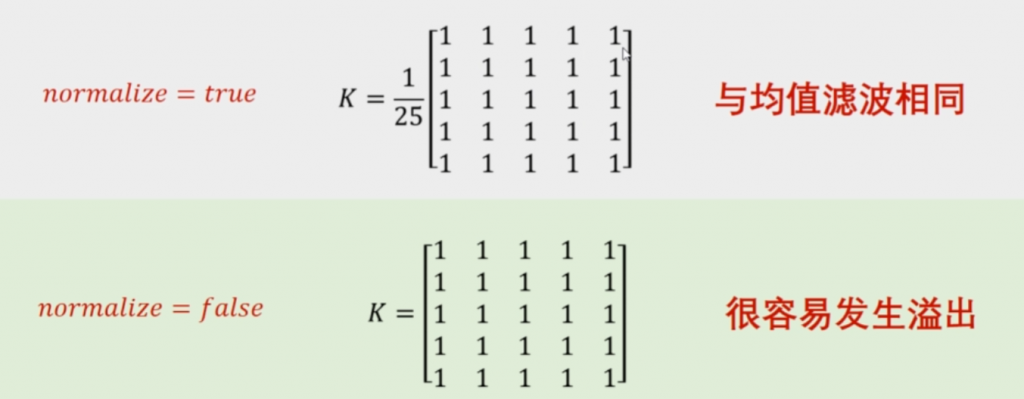
#处理结果 = cv2.boxFilter(原始图像， 目标图像深度，核大小， normalize属性)
#目标图像深度： int类型的目标图像深度，通常用-1表示与原始图像一致。
#normalize属性：是否对目标图像进行归一化处理。

img2 = cv2.boxFilter(img1, -1, (5, 5), normalize = 1) #归一化处理，与均值滤波相同，若省略则默认为1（true）

3.高斯滤波

让邻近的像素具有更高的重要度。对周围的像素计算加权平均值，较近的像素具有较大的权重值。

既然名称为高斯滤波器，那么其和高斯分布（正态分布）是有一定的关系的。一个二维的高斯函数如下：

h(x,y) = e ^ {- \frac{x^2 + y^2}{2\sigma ^ 2}}

其中(x,y)(x,y)为点坐标，在图像处理中可认为是整数；σ是标准差。要想得到一个高斯滤波器的模板，可以对高斯函数进行离散化，得到的高斯函数值作为模板的系数。例如：要产生一个3×3的高斯滤波器模板，以模板的中心位置为坐标原点进行取样。模板在各个位置的坐标，如下所示（x轴水平向右，y轴竖直向下）

这样，将各个位置的坐标带入到高斯函数中，得到的值就是模板的系数。
对于窗口模板的大小为 (2k+1)×(2k+1)，模板中各个元素值的计算公式如下：

H_{i,j} = \frac{1}{2\pi \sigma ^ 2}e ^{-\frac{(i - k - 1)^2 + (j - k - 1)^2}{2 \sigma ^ 2}}

这样计算出来的模板有两种形式：小数和整数。

• 小数形式的模板，就是直接计算得到的值，没有经过任何的处理；
• 整数形式的，则需要进行归一化处理，将模板左上角的值归一化为1，下面会具体介绍。使用整数的模板时，需要在模板的前面加一个系数，系数为模板系数和的倒数

\frac{1}{\sum\limits_{(i,j)\in w}w_{i,j}}

更多原理，参考https://www.cnblogs.com/wangguchangqing/p/6407717.html

#img2 = cv2.GaussianBlur(img1, ksize, sigmaX)
#ksize: 核大小(N, N) 必须是奇数
#sigmaX: X方向方差，控制权重
#sigmaX = 0时: sigma = 0.3 * ((ksize-1) * 0.5 - 1) + 0.8

img2 = cv2.GaussianBlur(img1, (3, 3), 0)

4.中值滤波

让临近的像素按照大小排列，去排序像素集中位于中间位置的值作为中值滤波后的像素值。对于椒盐图的处理，中值滤波的效果最好。

#img2 = cv2.medianBlur(img1, ksize)
#ksize：核大小，必须是比1大的奇数，如3，5，7等

img2 = cv2.medianBlur(img1, 3)

• OpenCV
• 计算机视觉