OpenCV学习笔记(6)——图像金字塔
- 蒙面西红柿
- 16,850
原理
图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度像素采样的方式,生成N个不同分辨率的图像。把具有最高级别分辨率的图像放在底部,以金字塔形状排列,往上是一系列像素(尺寸)逐渐降低的图像,一直到金字塔的顶部只包含一个像素点的图像,这就构成了传统意义上的图像金字塔。
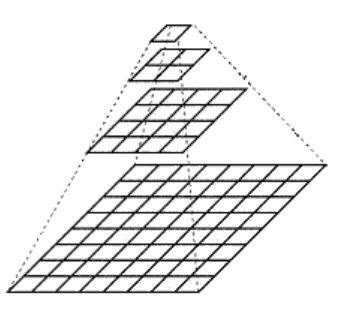
生成图像金字塔主要包括两种方式——向下取样(缩小图像),向上取样(放大图像)。向下取样是分辨率越来越小;向上取样是增加像素。
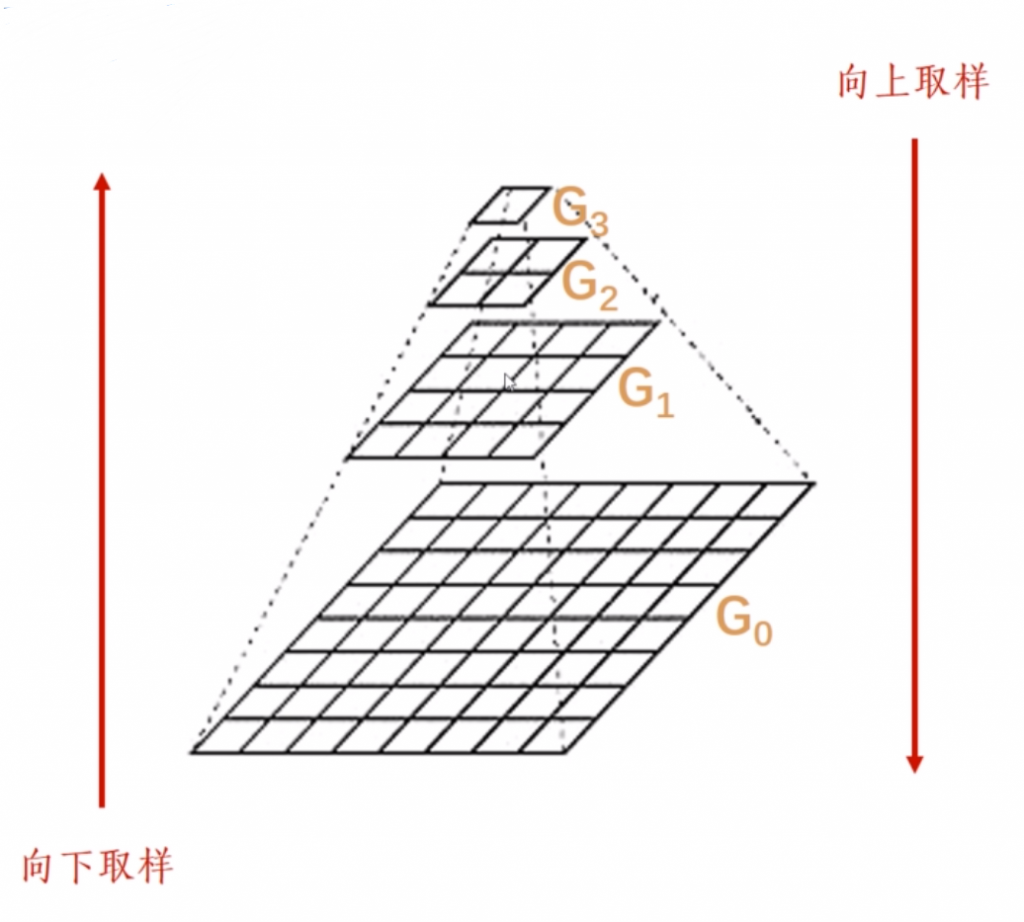
1. 高斯金字塔
向下取样:Gi -> Gi+1
- 对图像Gi进行高斯核卷积。
- 删除所有的偶数行和列。
每次处理以后,结果图像是原来的四分之一(M/2 * N/2)。上述操作被称为Octave。
向上取样: Gi -> Gi-1
- 将图像在每个方向扩大为原来的两倍,新增的行和列以0填充。
- 使用先前同样的卷积核乘以四与放大后的图像卷积,获得 “新增像素”的近似值。
乘以四的卷积核例子:
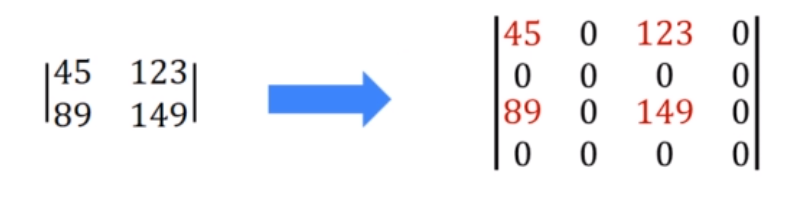
上图的像素45如果正常卷积,会变成45/4,因为周围都是新增像素0。为了能使图像正确,必须在卷积核乘以4来还原颜色。
得到的图像即为放大后的图像,但是与原来的图像相比会发觉比较模糊,因为在缩放的过程中已经丢失了一些信息,如果想在缩小和放大整个过程中减少信息的丢失,这些数据形成了拉普拉斯金字塔。
1.1 SIFT中的高斯金字塔*
高斯金字塔式在Sift算子中提出来的概念,首先高斯金字塔并不是一个金字塔,而是有很多组(Octave)金字塔构成,并且每组金字塔都包含若干层(Interval)。
高斯金字塔的构建过程:
1. 先将原图像扩大一倍之后作为高斯金字塔的第1组第1层,将第1组第1层图像经高斯卷积(其实就是高斯平滑或称高斯滤波)之后作为第1组金字塔的第2层,高斯卷积函数为:
G(x,y)=\frac{1}{2\pi \sigma ^2}e^{-\frac{(x-x_0)^2+(y-y_0)^2}{2\sigma ^2}}对于参数σ,在Sift算子中取的是固定值1.6。
2. 将σ乘以一个比例系数k,等到一个新的平滑因子σ=k*σ,用它来平滑第1组第2层图像,结果图像作为第3层。
3. 如此这般重复,最后得到L层图像,在同一组中,每一层图像的尺寸都是一样的,只是平滑系数不一样。它们对应的平滑系数分别为:
0,σ,kσ,k^2σ,k^3σ……k^{L-2}σ4. 将第1组倒数第三层图像作比例因子为2的降采样,得到的图像作为第2组的第1层,然后对第2组的第1层图像做平滑因子为σ的高斯平滑,得到第2组的第2层,就像步骤2中一样,如此得到第2组的L层图像,同组内它们的尺寸是一样的,但是在尺寸方面第2组是第1组图像的一半。
这样反复执行,就可以得到一共O组,每组L层,共计O*L个图像,这些图像一起就构成了高斯金字塔,结构如下:

1.2高斯金字塔在OpenCV调用
向下取样:
#img2 = cv2.pyrDown(img1)
img2 = cv2.pyrDown(img1)
img3 = cv2.pyrDown(img2)
img4 = cv2.pyrDown(img3)向上取样:
#img2 = cv2.pyrUp(img1)
img2 = cv2.pyrUp(img1)
img3 = cv2.pyrUp(img2)
img4 = cv2.pyrUp(img3)2. 差分金字塔*
DOG(Difference of Gaussian)金字塔是在高斯金字塔的基础上构建起来的,其实生成高斯金字塔的目的就是为了构建DOG差分金字塔。
构建过程:
差分金字塔的第1组第1层是由高斯金字塔的第1组第2层减第1组第1层得到的。以此类推,逐组逐层生成每一个差分图像,所有差分图像构成差分金字塔。括为差分金字塔的第o组第l层图像是有高斯金字塔的第o组第l+1层减第o组第l层得到的。
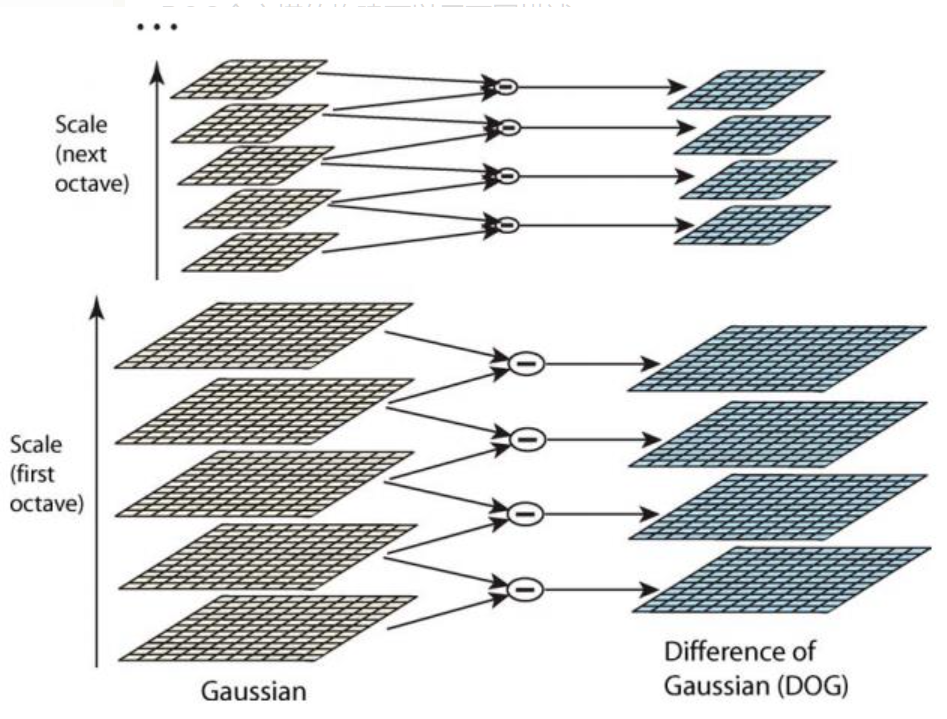
结果都是黑的,人眼看不到效果。实际计算结果包含了大量信息点。
我们对结果进行归一化操作,此时就变成了laplace金字塔了。
3.拉普拉斯金字塔
3.1 拉普拉斯金字塔原理
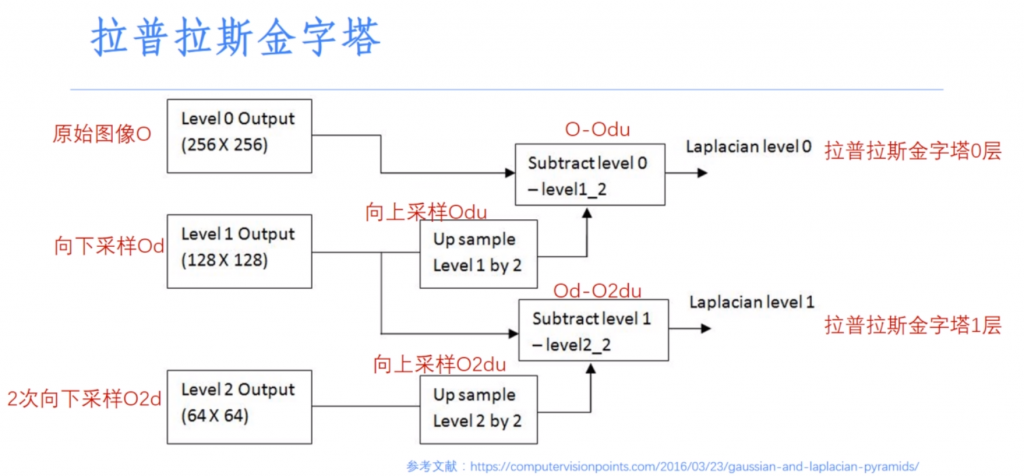
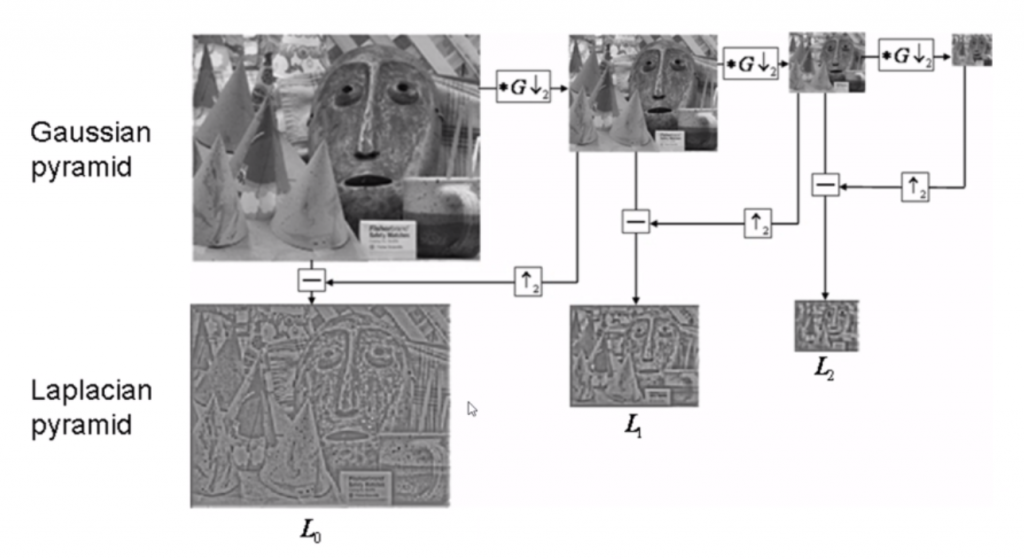
3.2 拉布拉斯金字塔在OpenCV的调用
#img2 = img1 - PyrUp(PyrDown(img1))
#第0层
img1d = cv2.pyrDown(img1)
img1u = cv2.pyrUp(img1d)
lap0 = img1 - img1u
img2 = img1d
#第1层
img2d = cv2.pyrDown(img2)
img2u = cv2.pyrUp(img2d)
lap1 = img2 - img2u
img3 = img2d

文章评论
Say, you got a nice post. Really looking forward to read more. Really Great. Vivia Leon Oberg
A round of applause for your blog post. Really looking forward to read more. Much obliged. Aliza Abeu Wilmott
Appreciating the persistence you put into your site and detailed information you provide. Mallissa Alaric Hieronymus
I need to to thank you for this good read!! I certainly loved every bit of it. Daisie Tann Fleck
gerçekten güzel bir yazı olmuş. Yanlış bildiğimiz bir çok konu varmış. Teşekkürler.
very informative articles or reviews at this time.