贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法。
1 分类问题综述
对于分类问题,其实谁都不会陌生,日常生活中我们每天都进行着分类过程。例如,当你看到一个人,你的脑子下意识判断他是学生还是社会上的人;你可能经常会走在路上对身旁的朋友说“这个人一看就很有钱”之类的话,其实这就是一种分类操作。
既然是贝叶斯分类算法,那么分类的数学描述又是什么呢?
从数学角度来说,分类问题可做如下定义:已知集合C = y^1, y^2, y^3,... , y^n和 I = x^1, x^2, x^3,..., x^n,确定映射规则y = f(x),使得任意x^i ∈ I有且只有一个y^i ∈ C,使得y^i ∈ f(x^i)成立。
其中C叫做类别集合,其中每一个元素是一个类别,而I叫做项集合(特征集合),其中每一个元素是一个待分类项,f叫做分类器。分类算法的任务就是构造分类器f。
分类算法的内容是要求给定特征,让我们得出类别,这也是所有分类问题的关键。那么如何由指定特征,得到我们最终的类别,也是我们下面要讲的,每一个不同的分类算法,对应着不同的核心思想。
本篇文章,我会用一个具体实例,对朴素贝叶斯算法几乎所有的重要知识点进行讲解。
2 朴素贝叶斯分类
那么既然是朴素贝叶斯分类算法,它的核心算法又是什么呢?
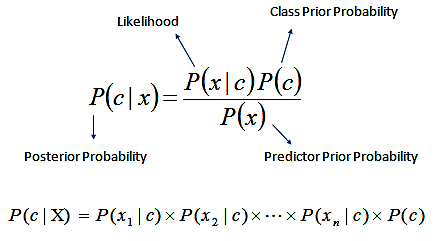
下面是贝叶斯公式:
P(B|A) = \dfrac{P(A|B)P(B)}{P(A)}
换个表达形式就会明朗很多,如下:
P(类别|特征) = \dfrac{P(特征|类别)P(类别)}{P(特征)}
最终的目的是求得p(类别|特征)。
3 例题分析
下面我先给出例子问题。给定数据如下:
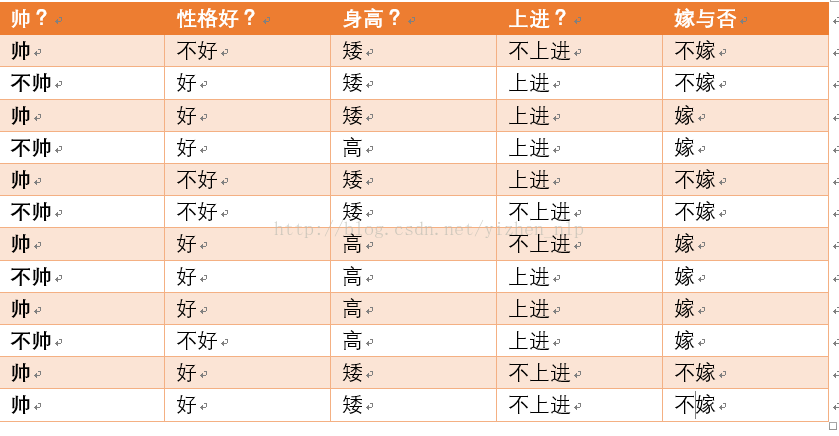
现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!
这里我们联系到朴素贝叶斯公式:
P(嫁|不帅,性格不好,身高矮,不上进) = \dfrac{P(不帅,性格不好,身高矮,不上进|嫁)P(嫁)}{P(不帅,性格不好,身高矮,不上进)}
我们需要求P(嫁|不帅,性格不好,身高矮,不上进)
这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量。
P(不帅,性格不好,身高矮,不上进|嫁),P(不帅,性格不好,身高矮,不上进)P(嫁)(至于为什么能求,后面会讲,那么就太好了,将待求的量转化为其它可求的值,这就相当于解决了我们的问题!)
4 朴素贝叶斯算法的朴素一词解释
那么这三个量是如何求得?
是根据已知训练数据统计得来,下面详细给出该例子的求解过程。回忆一下我们要求的公式如下:
P(嫁|不帅,性格不好,身高矮,不上进) = \dfrac{P(不帅,性格不好,身高矮,不上进|嫁)P(嫁)}{P(不帅,性格不好,身高矮,不上进)}
那么我只要求得P(不帅,性格不好,身高矮,不上进|嫁),P(不帅,性格不好,身高矮,不上进)P(嫁)即可,好的,下面我分别求出这几个概率,最后一比,就得到最终结果。
P(不帅、性格不好、身高矮、不上进|嫁) = P(不帅|嫁)P(性格不好|嫁)P(身高矮|嫁)P(不上进|嫁),那么我就要分别统计后面几个概率,也就得到了左边的概率!
等等,为什么这个成立呢?学过概率论的同学可能有感觉了,这个等式成立的条件需要特征之间相互独立吧!
对的!这也就是为什么朴素贝叶斯分类有朴素一词的来源,朴素贝叶斯算法是假设各个特征之间相互独立,那么这个等式就成立了!
由此,我们将(嫁|不帅、性格不好、矮、不上进)转换成三个可求的P(嫁)、P(不帅、性格不好、矮、不上进|嫁)、P(不帅、性格不好、矮、不上进)。进一步分解可以得:
P(不帅、性格不好、矮、不上进)=P(嫁)P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)+P(不嫁)P(不帅|不嫁)P(性格不好|不嫁)P(矮|不嫁)P(不上进|不嫁)。
P(不帅、性格不好、矮、不上进|嫁)=P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)
将上面的公式整理一下可得:

P(嫁)=1/2、P(不帅|嫁)=1/2、P(性格不好|嫁)=1/6、P(矮|嫁)=1/6、P(不上进|嫁)=1/6。
P(不嫁)=1/2、P(不帅|不嫁)=1/3、P(性格不好|不嫁)=1/2、P(矮|不嫁)=1、P(不上进|不嫁)=2/3。
但是由贝叶斯公式可得:对于目标求解为不同的类别,贝叶斯公式的分母总是相同的。所以,只求解分子即可:
于是,对于类别“嫁”的贝叶斯分子为:P(嫁)P(不帅|嫁)P(性格不好|嫁)P(矮|嫁)P(不上进|嫁)=1/2 * 1/2 * 1/6 * 1/6 * 1/6=1/864
对于类别“不嫁”的贝叶斯分子为:P(不嫁)P(不帅|不嫁)P(性格不好|不嫁)P(矮|不嫁)P(不上进|不嫁)=1/2 * 1/3 * 1/2 2/3=1/18。
经代入贝叶斯公式可得:P(嫁|不帅、性格不好、矮、不上进)=(1/864) / (1/864+1/18)=1/49=2.04%
P(不嫁|不帅、性格不好、矮、不上进)=(1/18) / (1/864+1/18)=48/49=97.96%
则P(不嫁|不帅、性格不好、矮、不上进) > P(嫁|不帅、性格不好、矮、不上进),因此该女子选择不嫁。
5 朴素贝叶斯的优缺点
优点:
1. 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
2. 分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
缺点:
朴素贝叶斯假设属性之间相互独立,这种假设在实际过程中往往是不成立的。在属性之间相关性越大,分类误差也就越大。
来源:

文章评论
这个公式太扎心了